Interpreting the U and S curves generated by WarpPLS

Linear relationships between pairs of latent variables, that is, those relationships best described by a line, are relatively easy to interpret. They suggest that an increase in one variable either leads to an increase (if the slope of the line is positive) or decrease (if the slope is negative) in the other variable.

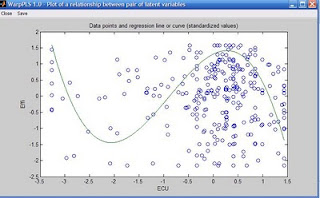
Nonlinear relationships provide a much more nuanced view of the data, but at the same time are much more difficult to interpret correctly. The graph below (click on it to enlarge) shows an S curve that is fitted to the data represented by the dots (or small circles) plotted in a scattered way on the graph. The latent variables are “ECU”, the extent to which electronic communication media are used by a team charged with developing a new product; and “Effi”, the efficiency of the team.

As you can see, the S curve is actually a combination of two U curves, one straight and the other inverted, connected at an inflection point. The inflection point is the point at the curve where the curvature, or second derivative of the S curve, changes direction. On the graph shown above, the inflection point is located at around minus 1 standard deviations from the "ECU" mean. That mean is at the zero mark on the horizontal axis.

Because an S curve is a combination of two U curves, we can interpret each U curve section separately. A straight U curve, like the one shown on the left side of the graph, before the inflection point, can be interpreted as follows.

The first half of the U curve goes from approximately minus 3.4 to minus 1.9 standard deviations from the mean, at which point the lowest team efficiency value is reached for the U curve. In that first half of the U curve, an increase in electronic communication media use leads to a decrease in team efficiency. After that first half, an increase in electronic communication media use leads to an increase in team efficiency.

One interpretation is that the first half of the U curve refers to novice users of electronic communication media. That is, novice users struggling to use more and more intensely communication media that they are not familiar with end up leading to efficiency losses for the team. At a certain point, around minus 1.9 standard deviations, that situation changes, and the teams start to really benefit from the use of electronic communication media, possibly because the second half of the U curve refers to users with more experience in using the media.

The interpretation of the second, inverted U curve, should be done in a similar fashion. As you can see, it is not easy to interpret nonlinear relationships. But the apparent simplicity of linear estimations of nonlinear relationships, which is usually what is done by other structural equation modeling software, is nothing but a mirage.

Field studies, small samples, and WarpPLS

Let us assume that a researcher wants to evaluate the effectiveness of new management method by conducting an intervention study in one single organization.

In this example, the researcher facilitates the use of a new management method by 20 managers in the organization, and then measures their degree of adoption of the method and their effectiveness.

The above is an example of a field study. Often field studies will yield small datasets, which will not conform to parametric analysis (e.g., ANOVA and ordinary multiple regression) pre-conditions. For example, the data will not typically be normally distributed.

WarpPLS can be very useful in the analysis of this type of data.

One reason is that, with small sample sizes, it may be difficult to identify linear relationships that are strong enough to be statistically significant (at P lower than 0.05, or less). Since WarpPLS implements nonlinear analysis algorithms, it can be very useful in the analysis of small samples.

Another reason is that P values are calculated through resampling, a nonparametric approach to statistical significance estimation. For small samples (i.e., lower than 100), jackknifing is the recommended resampling approach. Bootstrapping is recommended only for sample sizes greater than 100.

Standard deviation is not the same as range of variation

Means and standard deviations can be generated and saved through the “Save grouped descriptive statistics into a tab-delimited .txt file” option of WarpPLS. You can choose a grouping variable, number of groups, and the variables to be grouped. This option is useful if one wants to conduct a comparison of means analysis using the software, where one variable (the grouping variable) is the predictor, and one or more variables are the criteria (the variables to be grouped).

In comparisons of means analyses, research results are normally expressed in means and standard deviations. For example, in the study reviewed in this post, it is stated that the weight of participants in a 12-week weight loss study varied from: 87.9 plus or minus 15.4 kg (at baseline, or before the 12-week intervention) to 81.7 plus or minus 16.2 kg (after the 12-week intervention).

The 87.9 and 81.7 are the average weights (a.k.a. “mean” weights), in kilograms, before and after the 12-week intervention. However, the 15.4 and 16.2 are NOT the range of variation in weights around the means before and after 12-week intervention. They are actually the ranges around the means encompassing approximately 68 percent of all of the values measured (see figure below, from www.electrical-res.com).

In the figure above, the minus and plus 15.4 and 16.2 values would be the “mean(x) – s” and “mean(x) + s” points on the horizontal axis of histograms of weights plotted before and after the 12-week intervention. This assumes that the distributions of weights are normal, or quasi-normal (i.e., similar to a bell-shaped, or normal, curve); a common assumption in this type of research.

The larger the standard deviation, the wider is the variation in the measures, and the flatter is the associated histogram (the bell-shaped curve). This property has a number of interesting implications, some of which will be discussed in other posts.

Sometimes another measure of dispersion, the variance, is reported instead of the standard deviation. The variance is the standard deviation squared.

The reason why standard deviations are reported instead of ranges of variation is that outliers (unusually high or low values) can dramatically widen the ranges. The standard deviation coefficient is much less sensitive to outliers.

Geographically distributed collaborative SEM analysis using WarpPLS

I am currently conducting a geographically distributed collaborative SEM analysis using WarpPLS. The analysis involves a few people in different states of the USA, and two people outside the country. The collaborators are not only separated by large distances, but also operate in different time zones.

Yet, we have no problems collaborating. The collaboration is asynchronous – one person does some work one day, and shares it with the others, who review the work in the next few days and respond.

Since we all have WarpPLS installed on our computers, we exchange different versions of a WarpPLS project file (extension “.prj”) with the same dataset. This way we can do analyses in turns, and discuss the results on emails.

Each slightly different project file is saved with a different name – e.g., W3J_InfoOvld_2010_03_02.prj, W3B_InfoOvld_2010_03_02.prj, W2J_InfoOvld_2010_03_02.prj etc.

In the examples above, the first three letters indicate the SEM algorithm used (W3 = Warp3 PLS Regression; W2 = Warp2 PLS Regression), and the resampling method used (J = jackknifing; B = bootstrapping). The second part of the name describes the dataset, and the final part the date.

This is just one way of naming files. It works for our particular project, but more elaborate file names can be used in more complex collaborative SEM analyses.

This geographically distributed collaborative SEM analysis highlights one of the advantages of WarpPLS over other SEM software: all that is needed for the analysis is contained in one single project file.

Moreover, the project file will typically be only a few hundred kilobytes in size. In spite of its small size, the file includes the original data, and all of the results of the analysis.

One member of our team asked me how the project file can be so small. The reason is that all of the SEM analysis results are stored in a format that allows for their rendering every time they are viewed.

Plots of nonlinear relationships, for example, are not stored as bitmaps, but as equations that allow WarpPLS  to re-create those plots at the time of viewing.